Next: Forme canonique de la Up: Les espaces vectoriels Euclidiens Previous: Transformations orthogonales, isométries Contents Index
| Exercice n^&cir#circ;29 |
| matrices |
Soit 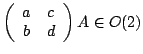 Calculer les conditions sur Calculer les conditions sur |


Calcul de ![]() et
et ![]() en fonction de
en fonction de ![]() et
et ![]() .
.

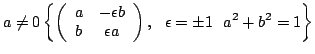
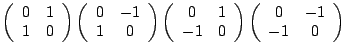


 équivaut a être sur le cercle trigonométrique.
équivaut a être sur le cercle trigonométrique.
Donc
![]()



Soit
![]() une isométrie,
une isométrie, ![]() la base canonique
la base canonique ![]() .
.
Si ![]() est valeur propre, alors
est valeur propre, alors
![]()
Si
![]() ,
,
![]() les vp de A (ou de u).
les vp de A (ou de u).
![]()
donc




Soit ![]() nouvelle base dans le plan
nouvelle base dans le plan ![]()
![]()


 est la matrice d'une rotation dans
est la matrice d'une rotation dans 
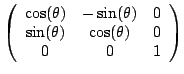
Watier Yves 2004-11-28