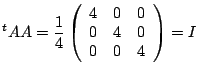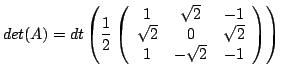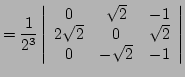Next: Interface Homme-Machine Up: Les espaces vectoriels Euclidiens Previous: Cas de et Contents Index
![]()
![]()
![]()
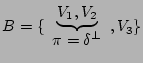
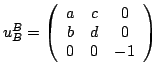
![]() donc
donc
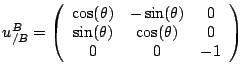
Composition de la symétrie par rapport à ![]() et de la rotation d'angle
et de la rotation d'angle ![]() d'axe
d'axe
![]()
| Exercice n^&cir#circ;30 |
| Identifier une isométrie |
Soit
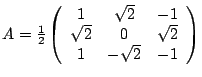
|