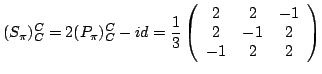Proection et symétries orthogonales

Soit le sev $F\subset E$, $E=F\oplus F^\bot$ càd que $\forall x \in E$. $x$ s'écrit comme $x=a+b$ avec $a\in F$ $b\in F^\bot$ écriture unique.

On définit la projection orthogonale sur F : $P_F:E \to E$ défini par $P_F(x) = a$.

$$P_F \centerdot P_F = P_F$$

$$Ker~P_F = F^\bot$$

$$Im~P_F = F$$

$$\forall x \in E, \forall y \in F ~~~\vert\vert x-P_F(x)\vert\vert\leq \vert\vert x-y\vert\vert$$

$$P_F(x) = (x\centerdot e_1)e_1 + \hdots + (x\centerdot e_p)e_p$$

On appelle symétrie orthogonale par rapport à F l'aplication linéaire $F_F:E\to E$

$$S_F(x) = 2P_F(x)-x=a-b$$

Ce qui de manière plus pratique pour les matrices:

$$S_F=2P_F-id$$

Propriétées $S_F rond S_F =id$
$S_{F^\bot}=-S_{F}$

Exercice n^&cir#circ;26

Symétries et projections

Soit d la droite engendrée par le vecteur $\left( \begin{array}{c} 1\\ 1 \end{array} \right )$
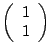
Donner la matrice de la projection sur la droite $P_d$
Donner la matrice de la symétrie sur la droite $S_d$ déduite de la projection.

On part de $\mathbb{R}^2 (C)\to \phi \to \mathbb{R}^2(C)$ et on cherche $\left(\left( \phi(e_1) \right) \right)$ càd la projection de $e_1$ dans $\{e_1;e_2\}$.
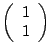Pbl: $\left( \begin{array}{c} 1\\ 1 \end{array} \right )$ n'est pas orthonormé.
On recherche la base orthonormée qui est $\left\lbrace \frac{1}{\sqrt{2}} \left( \begin{array}{c} 1\\ 1 \end{array} \right ) \right\rbrace$ V n'ayant qu'un vecteur.

$P_d(e_1) = (e_1 \centerdot V)V = \left( \frac{1}{\sqrt{2}} \left( \begin{array... ...ght ) \right) = \frac{1}{2} \left( \begin{array}{c} 1\\ 1 \end{array} \right )$

$P_d(e_1) = (e_1 \centerdot V)V = \left( \frac{1}{\sqrt{2}} \left( \begin{array... ...ght ) \right) = \frac{1}{2} \left( \begin{array}{c} 1\\ 1 \end{array} \right )$

$$(P_d)_C^C = \frac{1}{2} \left( \begin{array}{cc} 1&1\\ 1&1 \end{array} \right )$$

La symétrie maintenant :

$$(S_d)_C^C = 2 (P_d)_C^C - id = \frac{1}{2} \left( \begin{array}{c... ...\end{array} \right ) = \left( \begin{array}{cc} 0&1\\ 1&0 \end{array} \right )$$

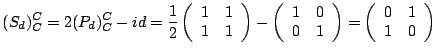
Exercice n^&cir#circ;27

Symétries et projections

Soit le plan de $\mathbb{R}^3$ d'equation $x_1 - 2x_2 + x_3=0$

1. Donner une base $B=\left\lbrace V_1 , V_2 , V_3 \right\rbrace$ orthonormée telle que $\left\lbrace V_1 , V_2\right\rbrace$ soit base de F.
2. Donner pour la base canonique de $\mathbb{R}^3$ les matrices d'applications $P_F$ et $S_F$.
3. Donner pour la base $B$ de $\mathbb{R}^3$ les matrices des applications $P_F$ et $S_F$.
4. Donner les matrices $id_C^B$ $id_B^C$ et retrouver 3) à parir de 2)

Soit $\pi = \left \lbrace \begin{array}{l} \left( \begin{array}{c} x_1\\ x_2\\ x_3 \end{array} \right ) \\ x_1- 2x_2 + x_3=0 \end{array} \right.$.
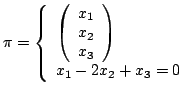$\left( \begin{array}{c} 1\\ -2\\ 1 \end{array} \right )$ est base de $\pi^\bot$.

On cherche 2 vecteurs ortohogonaux à $\left( \begin{array}{c} 1\\ -2\\ 1 \end{array} \right )$.

$\left( \begin{array}{c} 1\\ -2\\ 1 \end{array} \right ) \left( \begin{array}{c... ... 1 \end{array} \right ) \left( \begin{array}{c} 1\\ 1\\ 1 \end{array} \right )$

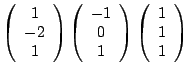
Orthonormés cela donne :
$B= \frac{1}{\sqrt{6}}\left( \begin{array}{c} 1\\ -2\\ 1 \end{array} \right ) \... ...ght ) \frac{1}{\sqrt{3}}\left( \begin{array}{c} 1\\ 1\\ 1 \end{array} \right )$

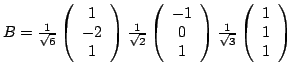
Une base de $\pi$ est $\frac{1}{\sqrt{2}}\left( \begin{array}{c} -1\\ 0\\ 1 \end{array} \right ) \frac{1}{\sqrt{3}}\left( \begin{array}{c} 1\\ 1\\ 1 \end{array} \right )$

$P_\pi(e_1) =(e_1 \centerdot V_1)V_1 + (e_2 \centerdot V_2)V_2 = \frac{1}{6}\left( \begin{array}{c} 5\\ 2\\ 1 \end{array} \right )$
$P_\pi(e_2) =\frac{1}{6}\left( \begin{array}{c} 2\\ 2\\ 2 \end{array} \right )$
$P_\pi(e_3) =\frac{1}{6}\left( \begin{array}{c} -1\\ 2\\ 5 \end{array} \right )$

$$(P_\pi)_C^C = \frac{1}{6} \left( \begin{array}{ccc} 5&2&-1\\ 2&2&2\\ -1&2&5 \end{array} \right )$$

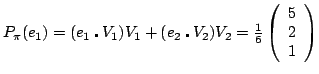
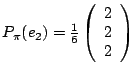
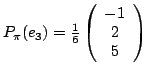
La symétrie maintenant :

$$(S_\pi)_C^C = 2 (P_\pi)_C^C -id = \frac{1}{3} \left( \begin{array}{ccc} 2&2&-1\\ 2&-1&2\\ -1&2&2 \end{array} \right )$$