Next: Proection et symétries orthogonales Up: Les espaces vectoriels Euclidiens Previous: Produits scalaires et bases Contents Index
Soit le sev
![]() ,
,
![]() , et soit
, et soit
![]() base orthonormée de
base orthonormée de ![]() alors il existe une base orthonormée
alors il existe une base orthonormée
![]() .
.
|
Si
|
| Exercice n^&cir#circ;24 |
| Recherche d'une base orthonormée |
On considère la droite 
Donner une base orthonormée de |
On cherche un vecteur non nul de ![]() répondant à l'équation, qu'on recoupera à la bonne norme aprés.
répondant à l'équation, qu'on recoupera à la bonne norme aprés.
On a forcément des multiples, on prend le plus simple:
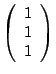 , il en faut deux autres 2 à 2 orthogonaux pour trouver la base, on cherche donc que le deuxième ait des coordonnées répondant à
, il en faut deux autres 2 à 2 orthogonaux pour trouver la base, on cherche donc que le deuxième ait des coordonnées répondant à
![]() d'ou
d'ou
 le troisième doit être orthogonal aux deux autres
le troisième doit être orthogonal aux deux autres
 .
.
Comme on les veut orthonormés de norme 1, on applique
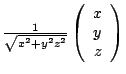 .
.
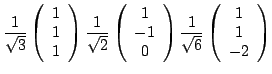
| Exercice n^&cir#circ;25 |
| Recherche d'une base orthonormée |
Trouver la base orthonormée de 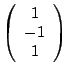 |
Proposition:
Soit
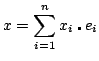
|
Watier Yves 2004-11-28