Next: Théorème d'existence des bases Up: Les espaces vectoriels Euclidiens Previous: Inégalités classiques Contents Index
Soit ![]() un ev,
un ev,
![]() base de
base de ![]() et
et
![]() .
.
Soient
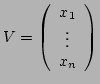 et
et
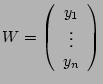 .
.
Proposition:

On cherche une base moins horrible cad qui soit plus adaptée aux scalaires.
Définition: On dit qu'une base est orthonormée si et seulement si on a:
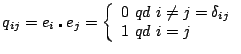
Si B est orthonormée
![]() .
.
Proposition:
E espave vectoriel + produit scalaire et
![]() famille de k vecteurs de E, telle que le
famille de k vecteurs de E, telle que le
![]() pout tout
pout tout ![]() ,
,![]() (2 à 2 orthogonaux) alors c'est une famille libre:
(2 à 2 orthogonaux) alors c'est une famille libre:
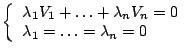
Dem :
![]()
![]()
En dévelloppant on enlève ceux dont le scalaire est nul (on a dit qu'il étaient orthogonaux deux à deux) on obtient:
| Exercice n^&cir#circ;22 |
| Famille libre de couples de vecteurs orthogonaux |
|
Soit E l'ensemble de fonctions:
Soit On considère sur E le produit scalaire: 
- Calculer la norme de chacun de ses vecteurs, afin de montrer qu'ils sont 2 à 2 orthogonaux. |
On a a calculer :
Pour les suivantes il faut se servir du formulaire des examens:
La 3 :
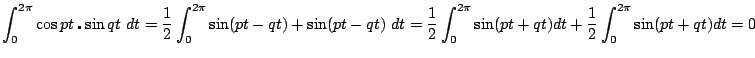
Même raisonnement pour la 4 la 5 et la 6.
Pour la norme il faut 2 fois le même vecteur:
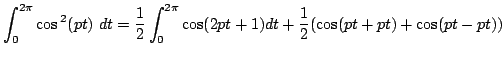
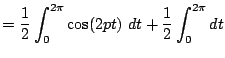
![$\displaystyle = \frac{1}{2}\left[ \frac{1}{2p} \sin(2pt) \right] _0^{2\pi} + \frac{1}{2}\left[ t \right] _0^{2\pi} $](img557.png)
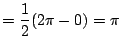
On trouve la même norme pour v (à faire).
![$\displaystyle \int_0^{2\pi}dt = \left[ t \right] _0^{2\pi} = 2\pi \Rightarrow \vert\vert u_0\vert\vert = \sqrt{2\pi}$](img560.png)
| Exercice n^&cir#circ;23 |
| Equations de l'hermitte |
|
Polynômes orthogonaux et équations aux dérivées partielles.
de plus on montre :
|

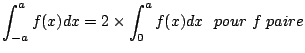
|
On sait que la fonction ![]() est paire, pour que
est paire, pour que
![]() soit impaire il suffit que
soit impaire il suffit que ![]() soit une fonction impaire.
soit une fonction impaire.
![]()
![]()
![]()
![]()
Il nous reste à calculer
![]() et
et
![]()
![]()
![]()
On en connait une partie, il suffit de calculer:
![]() et
et
![]()
A refaire,
![]() et
et
![]()
Watier Yves 2004-11-28