La géométrie liée aux produits scalaires, l'orthogonalité

Introduction

Rappels :

1. $\vec{V_1} = \left( \begin{array}{c} x_1\\ y_1 \end{array} \right )$ $\vec{V_2} = \left( \begin{array}{c} x_2\\ y_2 \end{array} \right )$
2. $\vec{V_1} \centerdot \vec{V_2} = x_1x_2 + y_1y_2$
3. $\vert\vert\vec{V} \vert\vert = \sqrt{x^2+y^2}$
4. $\vert\vert\vec{V} \vert\vert² = x^2+y^2$

Définitions

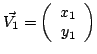
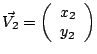
On appelle produit scalaire sur E une application de $E\times E \Rightarrow \mathbb{R}, (x,y) \to x\centerdot y$, telle que cette application est :

1. bilinéaire : $x \centerdot ( \alpha y + \beta y') = \alpha x \centerdot y + \beta x \centerdot y'$
2. symétrique : $x\centerdot y = y \centerdot x$
3. définie positive : $\forall x \in E$ $x\not=0$ $x\centerdot x>0$

Exercice n^&cir#circ;20

Produit scalaire et intégrales

Vérifier que : $f_1\centerdot f_2 = \int_a^b f_1(t)f_2(t)dt$, grâce à la définition du produit scalaire.

1. $$f_1 \centerdot ( \alpha f_2 + \beta f_3 ) = \int_a^b f_1(t) \times (\alpha f_2(t) + \beta f_3(t) )dt$$
   $$= \int_a^b \alpha f_1(t) f_2(t) dt + \int_a^b \beta f_1(t) f_3(t) dt$$
   Comme $\alpha$ et $\beta$ ne dépendent pas de t,
   $$= \alpha f_1 \centerdot f_2 + \beta f_1 \centerdot f_3$$

2. $$f_1 \centerdot f_2 = f_2 \centerdot f_1$$
   Trivial via les intégrales.

3. Prouver que c'est défini postif est compliqué.

Définitions

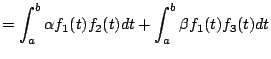
On appelle norme d'un vecteur $V$ (ou d'une fonction $V$) notée $\vert\vert V \vert\vert$ le nombre positif $\vert\vert V\vert\vert = \sqrt{V \centerdot V}$.
Par exemple pour $\mathbb{R}^3$ $V=\left( \begin{array}{c} x\\ y\\ z \end{array} \right )$ $\vert\vert V\vert\vert = \sqrt{x^2+y²+z²}$

$\forall V$ et $\forall W$ dans E

1. on a :

   $$\vert\vert V+W\vert\vert² = \vert\vert V\vert\vert² + \vert\vert W\vert\vert² +2 V \centerdot W$$
2. on dira que $V$ est orthogonal à $W$, noté $U \bot W$ ssi $V \centerdot W =0$
3. soient F et G sev de E les sev F et G sont dits orthogonaux ssi $\forall V \in F$ et $\forall X \in G$ on a $V \bot W$.
4. soit F un sev de E, on appelle orthogonal de F noté $F^\bot$.
   

   $$F^\bot = \left\lbrace V \in E \vert \forall W \in F~~V\centerdot W =0 \right\rbrace$$

   alors $F^\bot$ est un sev de E

?FIX ME:faire une phrase en fr? Dans un espace vectoriel ?truc?, toutes les droites passent par l'origine. Un affine permet d'avoir un décalage vers le haut de l'ensemble des droites (plan).