Next: Série de Fourier Up: Mathématiques Previous: Exemples Contents Index
Soit ![]() ,
,
![]() est la dérivée de
est la dérivée de ![]() pour y constant.
pour y constant.
![]() est la dérivée de
est la dérivée de ![]() pour x constant.
pour x constant.
Rappel: Théorème de Schwartz,
![]() .
.
| Exercice n^&cir#circ;3 |
| Dériver par rapport à y |
|
Soit
|
On a un produit, on dérive selon le shéma
![]() comme on recherche
comme on recherche
![]() , x est constant donc
, x est constant donc
![]() ,
,
![]() .
.
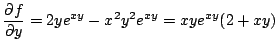
| Exercice n^&cir#circ;4 |
| Dériver par rapport à x |
|
Chercher
|
On dit que l'on a bien une fonction à deux variables séparées, car on a ![]() et pas par exemple
et pas par exemple ![]() .
.
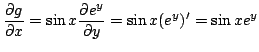
Watier Yves 2004-11-28