Next: Dérivées partielles Up: Equations différentielles à coefficients Previous: Solution générale Contents Index
| Exercice n^&cir#circ;1 |
| Sans second membre, deuxième degré |
|
Résoudre l'équation différentielle suivante
|
| Exercice n^&cir#circ;2 |
| Avec second membre, troisième degré |
|
Résoudre l'équation différentielle suivante
|

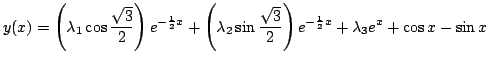
Watier Yves 2004-11-28