Next: Les espaces vectoriels Euclidiens Up: Expression complexe des séries Previous: Expression complexe des séries Contents Index
Le but est de s'affranchir de la périodicité ![]() , on passe de discret a continu en tendant l à l'infini.
, on passe de discret a continu en tendant l à l'infini.
Intégrale de Fourrier.
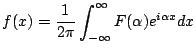
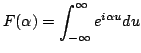
|
Soit ![]() tel que:
tel que:
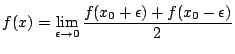

Alors :
Intégrale de Fourrier
![$\displaystyle f(x)=\int^\infty_{0} \left[ A(\alpha)\cos(\alpha x) + B(\alpha)\sin(\alpha x) \right] d \alpha $](img428.png)
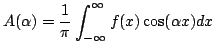
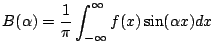
si |
| Exercice n^&cir#circ;17 |
| Une impulsion rectangulaire |
Soit
 Calculer
Calculer |
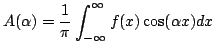

![$\displaystyle = \frac{2S}{\alpha \pi} \left[ \sin(\alpha x)\right] _0^k = \frac{2S}{\alpha \pi} \sin(\alpha k)$](img435.png)
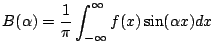
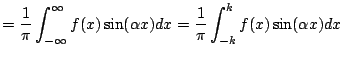
![$\displaystyle =\frac{S}{\alpha\pi} \left[ \cos(\alpha x) \right] _{-k}^k = \frac{S}{\alpha\pi}\times 0 = 0 $](img437.png)
![$\displaystyle f(x)=\int^\infty_{0} \left[ A(\alpha)\cos(\alpha x) + B(\alpha)\sin(\alpha x) \right] d \alpha $](img428.png)

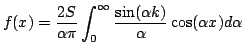
| Exercice n^&cir#circ;18 |
| Le retour de la barre métalique |
|
Cette fois ci la barre à une longueur infinie, l'origine est constamment à 0^&cir#circ;C.
Son équation de la chaleur est : 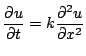

|
Par séparation des variables on obtient:
avec
![]() on trouve
on trouve
La somme ici sera alors :


![]() doit être impaire, on la définie sur
doit être impaire, on la définie sur
![]() avec
avec

La SG pour cette condition initiale est :
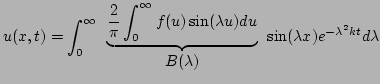

| Exercice n^&cir#circ;19 |
| Corde de longueur infinie |
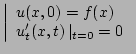

|
Watier Yves 2004-11-28