Next: IntÚgrale de Fourrier, transformÚe Up: MathÚmatiques Previous: Fonction de pÚriode Contents Index

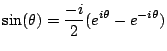
|
Pour l'étude d'une fonction qui est sur le schéma
![]() , on utilisera deux fonctions
, on utilisera deux fonctions
![]() telles que :
telles que :
alors
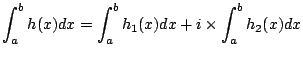


|
| Exercice n^&cir#circ;13 |
| Démonstration |
| Démontrer la propriété précédente |


Puis en mettant en facteur les ![]() on arrive à (!compléter!):
on arrive à (!compléter!):
![$\displaystyle \sum_{n=0}^\infty e^{\frac{i n \pi x}{l} } \left[ \frac{a_n - ib_...
...sum_{n=0}^\infty e^{-\frac{i n \pi x}{l} } \left[ \frac{a_n + ib_n}{2} \right]
$](img388.png)
![$\displaystyle a_n = \frac{1}{2 l} \int_{-l}^l f(x) \left( e^{\frac{i n \pi x}{l}} + e^{\frac{-i n \pi x}{l}} \right ] dx$](img389.png)
![$\displaystyle b_n = \frac{1}{2 l} \int_{-l}^l f(x) \left(-i e^{\frac{i n \pi x}{l}} + i e^{\frac{-i n \pi x}{l}} \right ] dx$](img390.png)
On remplace :


Avec ![]() :
:
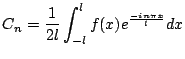
Identité de Perceval (somme des carrés des coefficients):
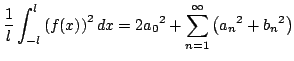
|
| Exercice n^&cir#circ;14 |
| Identité de Perceval |
|
Montrer que
|
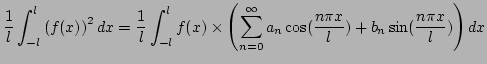


| Exercice n^&cir#circ;15 |
| Application de Parceval |
|
![$\displaystyle a_0 = \frac{1}{2} \int_{-1}^1 f(x) dx = \int_{0}^1 x dx = [ \frac{x┬▓}{2} ]_0^1 = \frac{1}{2}$](img404.png)
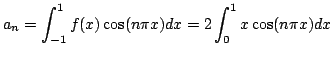
![$\displaystyle = \frac{2}{n┬▓\pi┬▓} [ \cos (n \pi x ) ]_0^1 = \frac{2}{n┬▓\pi┬▓} \left( (-1)^n -1 \right)$](img406.png)
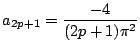

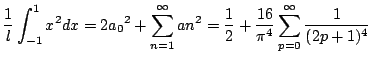
| Exercice n^&cir#circ;16 |
| Fourrier sous forme complexe |
Soit 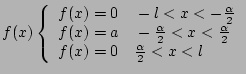
|
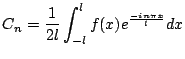
![$\displaystyle = \frac{a}{2l} \left[ \frac{l}{-in\pi}e^{\frac{-in\pi x}{l}} \right] ^\frac{\alpha}{2}_\frac{\alpha}{2} ~~~\vert n\not=0$](img413.png)
![$\displaystyle = \frac{a}{n\pi} \left[ \frac{i}{2}\left( e^{\frac{-in\pi\alpha}{2l}} - e^{\frac{+in\pi\alpha}{2l}}\right) \right] ~~~\vert n\not=0$](img414.png)
Il nous faut calculer la valeur pour ![]()

D'où



D'ou le dev de fourrier dans les Réels :
