Elle dépend de la forme du second membre.
- Cas ou le second membre est un polynôme de degré n.
- Si
 on cherche une solution particulière
on cherche une solution particulière 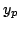 sous la forme d'un polynôme de degré
sous la forme d'un polynôme de degré 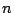 .
.
- Si
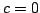 et
et 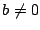 on cherche une solution particulière
on cherche une solution particulière 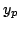 sous la forme d'un polynôme de degré
sous la forme d'un polynôme de degré  .
.
- Si
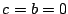 on integre 2 fois de suite le second membre.
on integre 2 fois de suite le second membre.
- Cas ou le second membre est de la forme
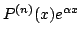 .
.
- Si
 n'est pas racine de
n'est pas racine de 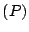 on cherche
on cherche 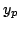 sous la forme
sous la forme

- Si
 est racine simple de
est racine simple de 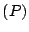 on cherche
on cherche 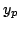 sous la forme
sous la forme
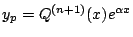
- Si
 est racine double de
est racine double de 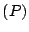 on cherche
on cherche 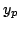 sous la forme
sous la forme
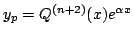
- Cas ou le second membre est de la forme
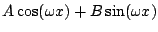 .
.
- Si
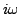 n'est pas racine de
n'est pas racine de 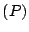 on cherche
on cherche 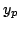 de la forme
de la forme
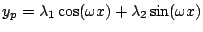 .
.
- Si
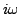 est racine de
est racine de 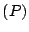 on cherche
on cherche 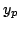 de la forme
de la forme
![$ y_p = \left[ \lambda_1 \cos(\omega x)+\lambda_2 \sin( \omega x)\right] \times x $](img107.png) .
.
Watier Yves
2004-11-28